Welcome the the MathNeuro website!
Our group is part of the Department of Mathematics and the Department of Neuroscience at UT Austin.
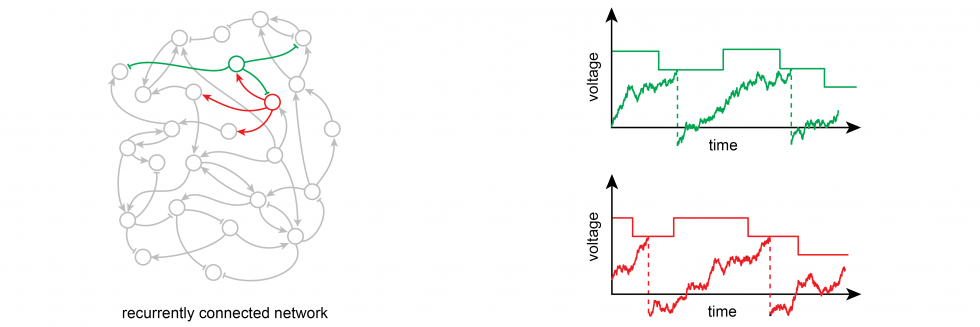
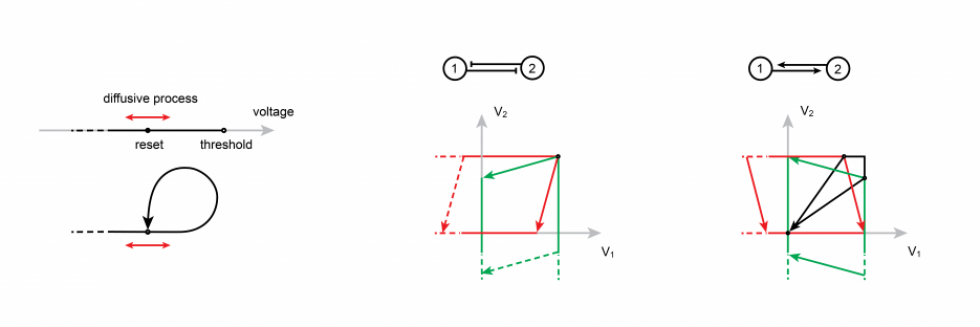
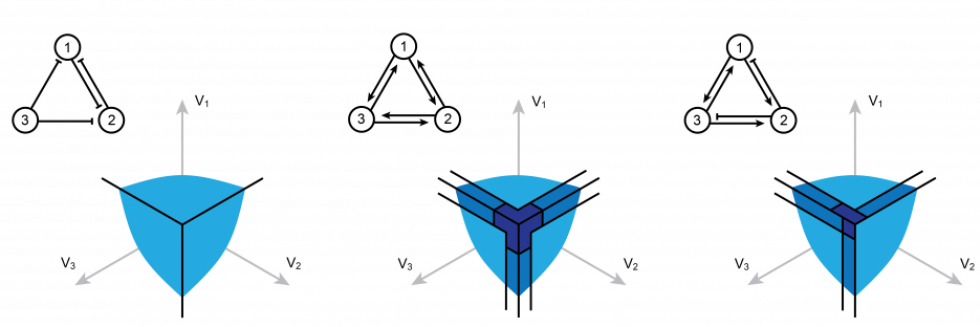
We are broadly interested in developing new theoretical approaches to better understand information processing in the brain. Working in close collaboration with experimental laboratories, we utilize techniques from stochastic dynamics, network theory, and information theory to analyze biophysically inspired models of neural networks.
We are accepting applications for postdoctoral positions as well as graduate students within the departments of Mathematics and Neuroscience.
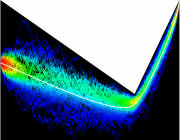
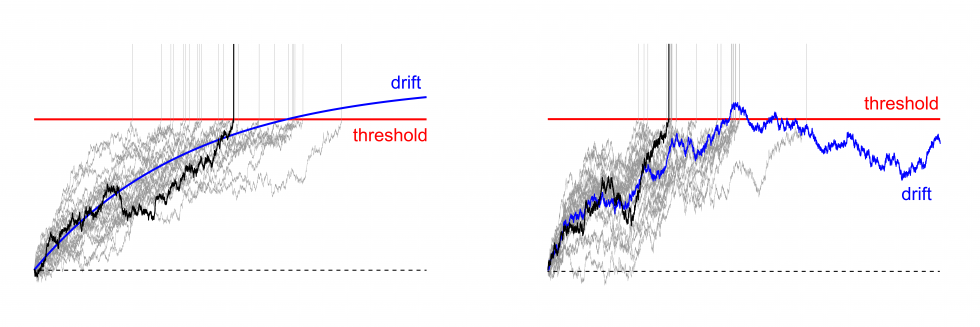
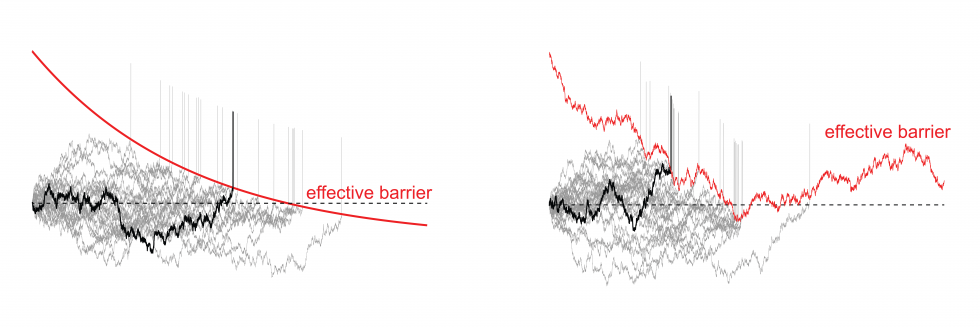
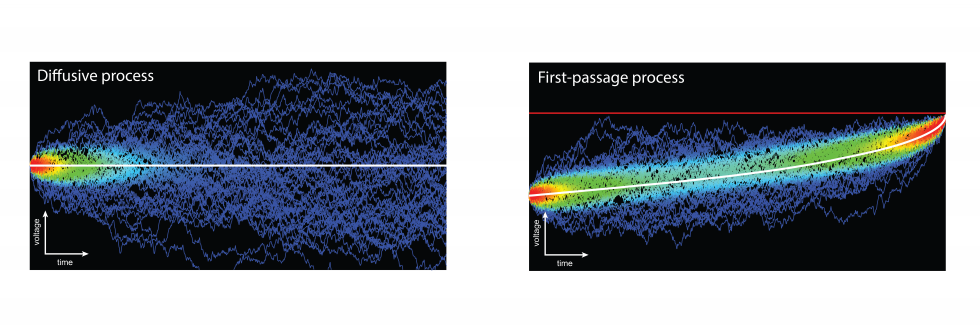
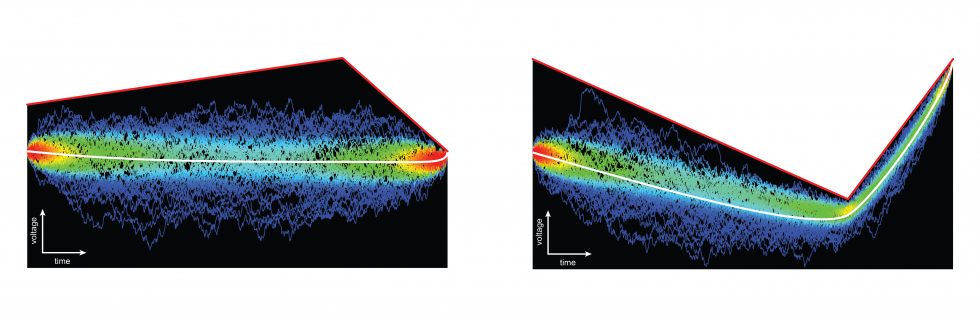
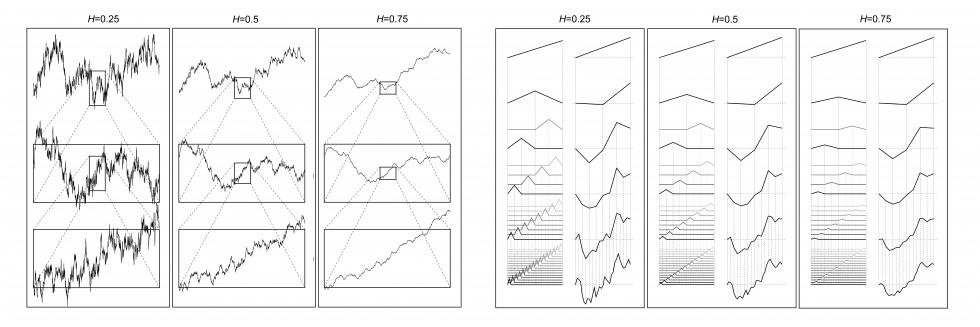
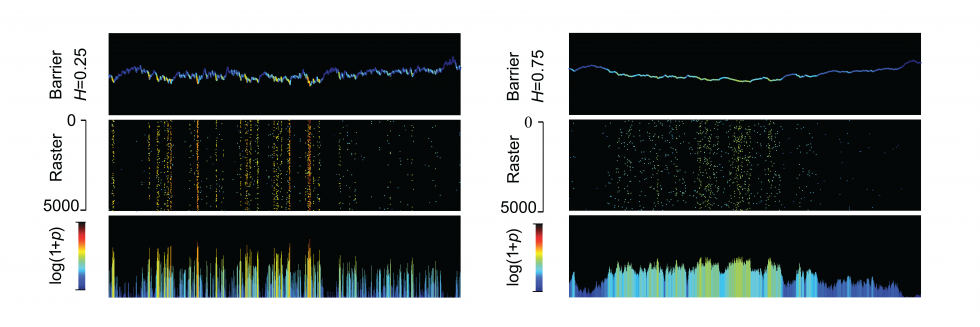
The above movie illustrates a Monte-Carlo algorithm that efficiently computes the first-passage time of a linear diffusion process with a straight boundary. Variations on this algorithm allow us to study numerically the distribution of spiking times for model neurons driven by fluctuating inputs.
The above movie illustrates the population dynamics of microbial cell types competing for three externally provided resources in a one dimensional space (top: resource concentrations, bottom: cell type populations). Competition between metabolic variants yields stationary states where consortia of distinct cell types achieve the maximum rate of biomass production.
Recent Publications
- Microbial consortia at steady supply
- Global solutions with infinitely many blowups in a mean-field neural network
- A structured scaffold underlies activity in the hippocampus
- Characterization of blowups via time change in a mean-field neural network
- Multistability in the replica-mean-field limit of spiking neural networks
- Place-cell capacity and volatility with grid-like inputs