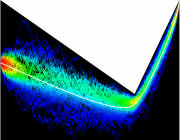
In the brain, neurons process information by propagating action potentials (or spikes) throughout complex neural networks. Deciphering the information carried by spiking patterns is the central question of neural coding. In principle, neural networks can encode information in countless different ways, each with their specific advantages or limitations in term of, e.g., noise reliability, information capacity, or energy efficiency. Within this context, a particularly relevant question is: Can the same neurons adopt different coding strategies? If so, what are the network-level parameters controlling the transition between codes?

We address these questions by focusing on two different encoding modalities, rate coding and time coding, which can be distinguished by the reliability and precision of neural spiking. This approach lead us to characterize the response of standard models for neurons (e.g. “integrate and fire”) to fluctuating inputs. In such models, the membrane potential of a neuron integrates the inputs and fluctuates due to biological noise; a spike occurs when the membrane potential exceeds a set threshold. For linear subthreshold dynamics, the spiking times of integrate-and-fire neurons are in fact first-passage times of diffusive trajectories with fluctuating barriers. The roughness of these fluctuating barriers is prescribed by the statistics of the afferent neural input.