Hippocampal place cells collectively generate a cognitive map of the physical world during spatial navigation. Concretely, a place cell is active when an animal passes some specific locations in an environment; those locations are called the place fields for that cell. Although these place fields are very sparse, they can encode for multiple locations in large environments. Place-cell codes with the highest capacity are those for which the maximum number of field configurations are possible for a given cell. In principle, the total number of possible configurations is astronomical.

However, place cells receive key inputs from the entorhinal cortex, where grid cells reside. These grid cells have regularly structured spatial responses with activity peaks arranged on periodic lattices, thereby representing a constrained number of possible inputs. Such constrained inputs must severely restrict the capacity of place-cell codes when other inputs are spatially uninformative or absent. The question of how input constraints restrict coding capacity is of general interest to any information processing system. Unfortunately, quantifying such restrictions resists classical theoretical methods as those used in machine learning. This is because these rely on the core assumption that inputs are unconstrained, as if randomly sampled from an unstructured distribution.

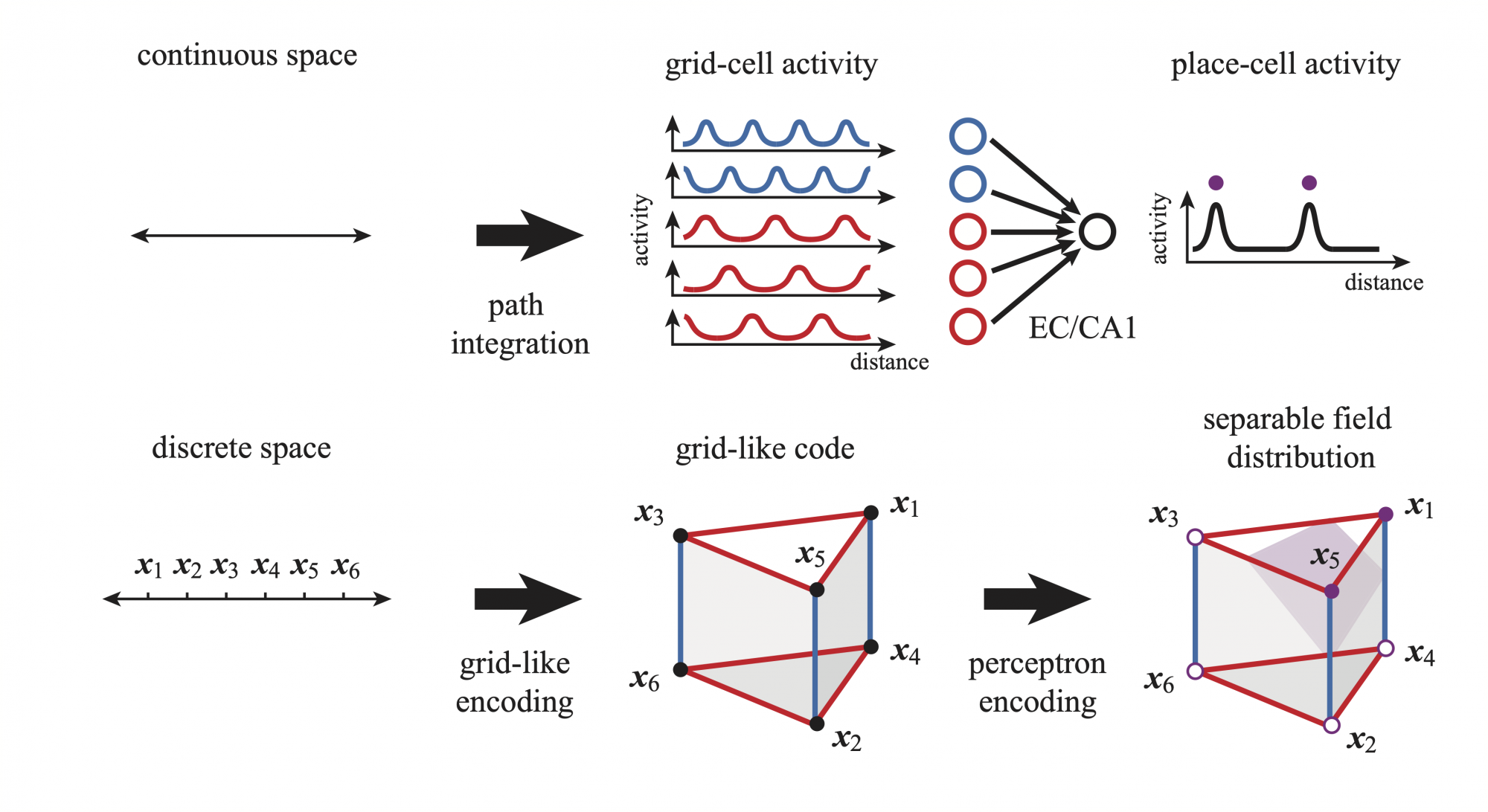
We addressed the above limitation by turning the problem of place-cell coding capacity into one of combinatorial geometry. Specifically, we considered determining the capacity of a neuron-inspired classifier, called perceptron, receiving oversampled lattice-structured, grid-like inputs. In this publication, we found that grid-like inputs represent the vertices of a highly symmetric solid in large dimension. Then considering grid-like inputs as a code within itself, without any reference to space, allowed us to exploit its many symmetries to geometrically solve our capacity problem. This problem consists in counting the number of ways with which one can separate the vertices of the solid by slicing it along a hyperplane. This is generally a NP-hard problem even for simple solid such as the hypercube. Luckily, we found that our problem can be solved satisfactorily for grid-like input, since the complexity of the problem is set by the limited number of distinct lattice periods of the inputs to a cell (2-3 periodic modules).

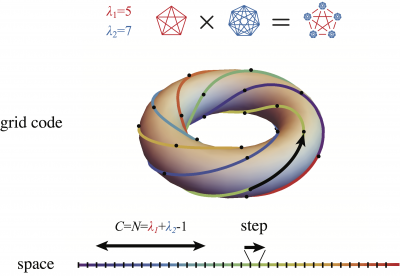
In practice, our results show that place cells can attain a large set of achievable field configurations, but nevertheless this number is a vanishing fraction of potential field configurations. The permitted field configurations tend to fall at highly constrained locations, which can be predicted by the geometry of grid-like inputs. We also show that place-field configurations driven by grid inputs, albeit fewer in number than potential configurations with random inputs, are more robust. Then, in this preprint, we validate this original theoretical study by detecting the statistical signature of the constraints imposed by grid-cell inputs. Specifically, we showed that for animals navigating in virtual environments without structured external cues, place fields tend to be distributed multiples-of-grid-periods away from one another, as predicted by theoretical and numerical analyses.