Artificial intelligence can now rival human performance in tasks such as speech or object recognition, language translation, and autonomous navigation. However, by contrast with artificial computations supported by fragile, hardwired circuits, biological computations appear to robustly emerge in noisy, disordered neural networks. Understanding how meaningful computations emerge from the seemingly random interactions of neural constituents remains a conundrum. To solve this conundrum, one can hope to mine biological networks for their design principles. Unfortunately, such a task is hindered by the sheer complexity of neural circuits. Deciphering neural computations will only be achieved through the simplifying lens of a biophysically relevant theory.

To date, neural computations have been studied theoretically in idealized models whereby an infinite number of neurons communicate via vanishingly small interactions. Such an approach neglects that neural computations are carried out by a finite number of cells interacting via a finite number of synapses. This neglect precludes understanding how neural circuits reliably process information in spite of neural variability, which depends on these finite numbers. 
 

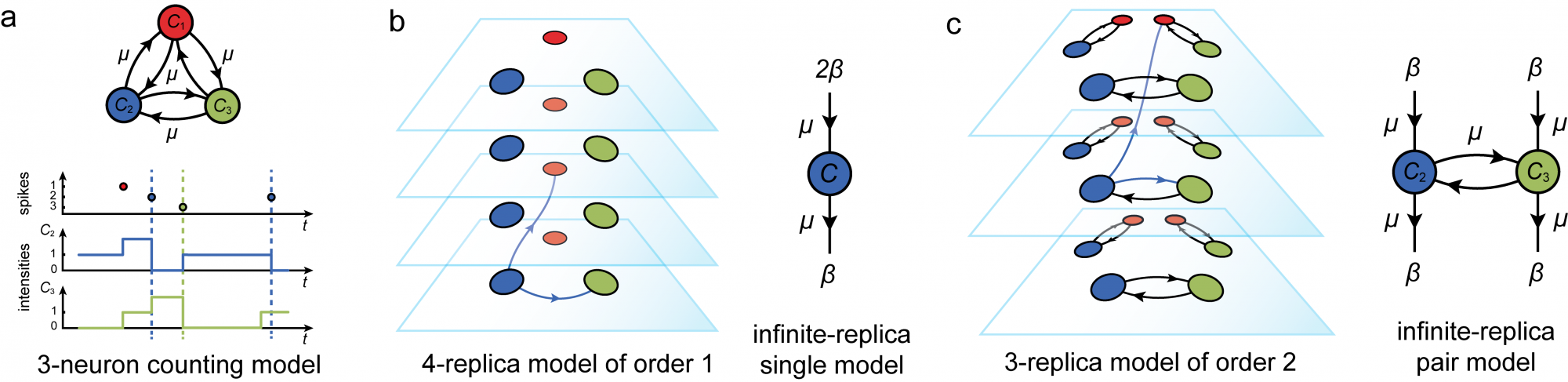
To remedy this point, we developped a novel theoretical framework allowing for the analysis of dynamics in neural circuits with finite-size structure: the replica-mean-field framework. Our approach leverages ideas from the theory of communication networks to understand how biophysically relevant network models can reliably process information via noisy, disordered circuits. In contrast to “divide and conquer” approaches, which equate a system with the mere sum of its parts, our approach decipher the activity of neural networks via a “multiply and conquer” approach. Concretely, this means that we consider limit networks made of infinitely many replicas with the same basic neural structure. The above figure sketches the core idea at stake: instead of trying to characterize the orignal network dynamics, one considers dynamics of replica network, whereby interactions among elementary constistuents (be they neurons or groups of neurons) are randomized across replicas. Replica-mean-field netwroks are obtained in the limit of an infinite number of replicas.

The key point is that these so-called replica-mean-field networks are in fact simplified, tractable versions of neural networks that retain important features of the finite network structure of interest. For more details, please check this publication, where we orginally introduced the core idea of replica-mean-field limits. An important feature of our approach is that there is a variety of replica-mean-field limits for the same finite network structure, many of which exhibit non trivial correlation activity. For more details, please check this publication, where we are able to predict pair-wise correlations for a restricted class of network structure.

Why caring so much about the finite-size structure of networks? I turns out that the finite size of neuronal populations and synaptic interactions is a core determinant of neural activity, being responsible for non-zero correlation in the spiking activity and for finite transition rates between metastable neural states. Accounting for these finite-size phenomena is actually the core motivation for the development of the replica approach. Our hope is to leverage the replica-mean-field network to gain a mechanistic understanding of the constraints bearing on computations in finite-size neural circuits, especially in terms of their reliability, speed, and cost. This will involve characterizing the finite-structure dependence of: (i) the regime of spiking correlations, which constrains the form of neural code and (ii) the transition rates between metastable neural states, which are thought to control the processing and gating of information. For more details about (i), please check this publication, and for more details about (ii), please check this publication.

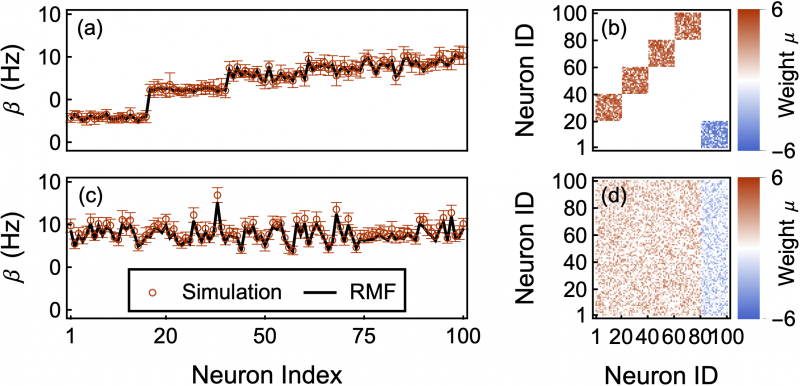
We are only starting to explore the replica-mean-field framework and we only recently demonstrated the mathematical property founding our approach, the asymptotic independence of replicas, for a large but restricted class of interacting, spiking dynamics. For more details, see this publication. We also have a whole research program to carry out computationally. Carrying out this program will crucially rely on the comparison between solutions to reduced functional equations, discrete-event simulations, and neural data sets. The ultimate goal will be to analyze biophysically detailed models in order to produce a fitting framework that is restrictive enough to formulate and validate experimental predictions.