The elementary computations of neural networks are understood on a physical and a chemical level. In the brain, neural networks process information by propagating all-or-none action potentials that are converted probabilistically at synapses between neurons. By contrast, the nature of neural computation at the network level – where thoughts are believed to emerge – remains largely mysterious. Do action potentials only “make sense” in the context of collective spiking patterns? Which spatiotemporal patterns constitute a “meaningful computation”? What neural codes make these computations possible in spite of biological noise?

To better understand neural computation, it is tempting to think of the brain by analogy as a modern-day communication networks and try to reverse-engineer it. Just like man-made devices, neural networks have to satisfy some design principles: On one hand maximizing the flow of information about the environment is beneficial to the survival of the organism. On the other hand, information processing in the brain is subject to severe biophysical and energy constraints. Indeed, current studies begin to show that the structure and function of neural networks have evolved to satisfy principles of efficient resource allocation and constraint minimization.

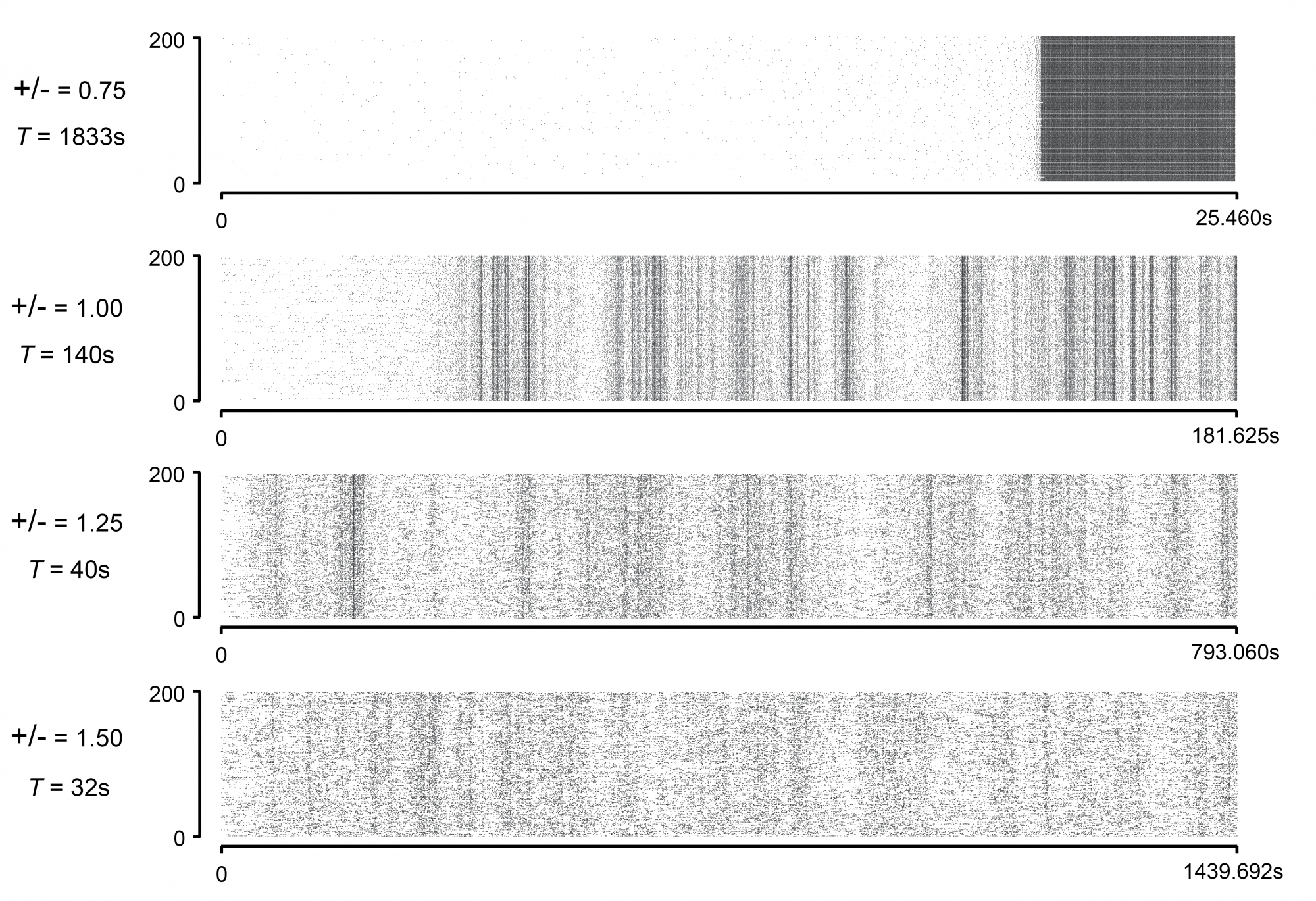
One thing that is missing in the field is a working model explaining how satisfying such principles constrains encoding strategies and network structures. We have begun to address this issue for networks of stochastic integrate-and-fire neurons, focusing on the transition from an asynchronous state, where neurons act as independent rate-coders, to a synchronous state, where neurons collectively act as time-coders. Interestingly, the transition between asynchronous and synchronous states, a critical phenomenon, appears to involve the break-down of time-reversal symmetry, which is the physical signature that computations are being performed.

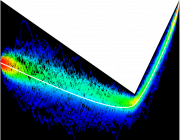
The above figure shows raster plots of the spiking activity of an unstructured network of integrate-and-fire neurons with delayed interactions and for different balance of excitation and inhibition. For large enough excitation, the dynamics of the network becomes critical and is driven by fluctuations.  We are interested in understanding the scaling properties of these fluctuations in relation with the structure of the network and of the driving input.

Understanding such transition is very challenging both computationally and theoretically. One of the main difficulty stems from the fact that as opposed to the asynchronous activity, synchronous activity represents a mathematically singular regime in stochastic neuronal models. In such models, a synchronous event is marked by the divergence of the population firing rate when approaching a given time, which triggers a finite fraction of the neurons to spike coincidentally. 

To elucidate this singular regime of activity, we recently proposed an idealized network model of integrate-and-fire neurons, the so-called Poissonian mean-field models, whereby synchrony can be studied analytically. The figure below summarizes the essential tenets of this model and introduces the trick that makes it analytically tractable: the existence of regularizing time change.

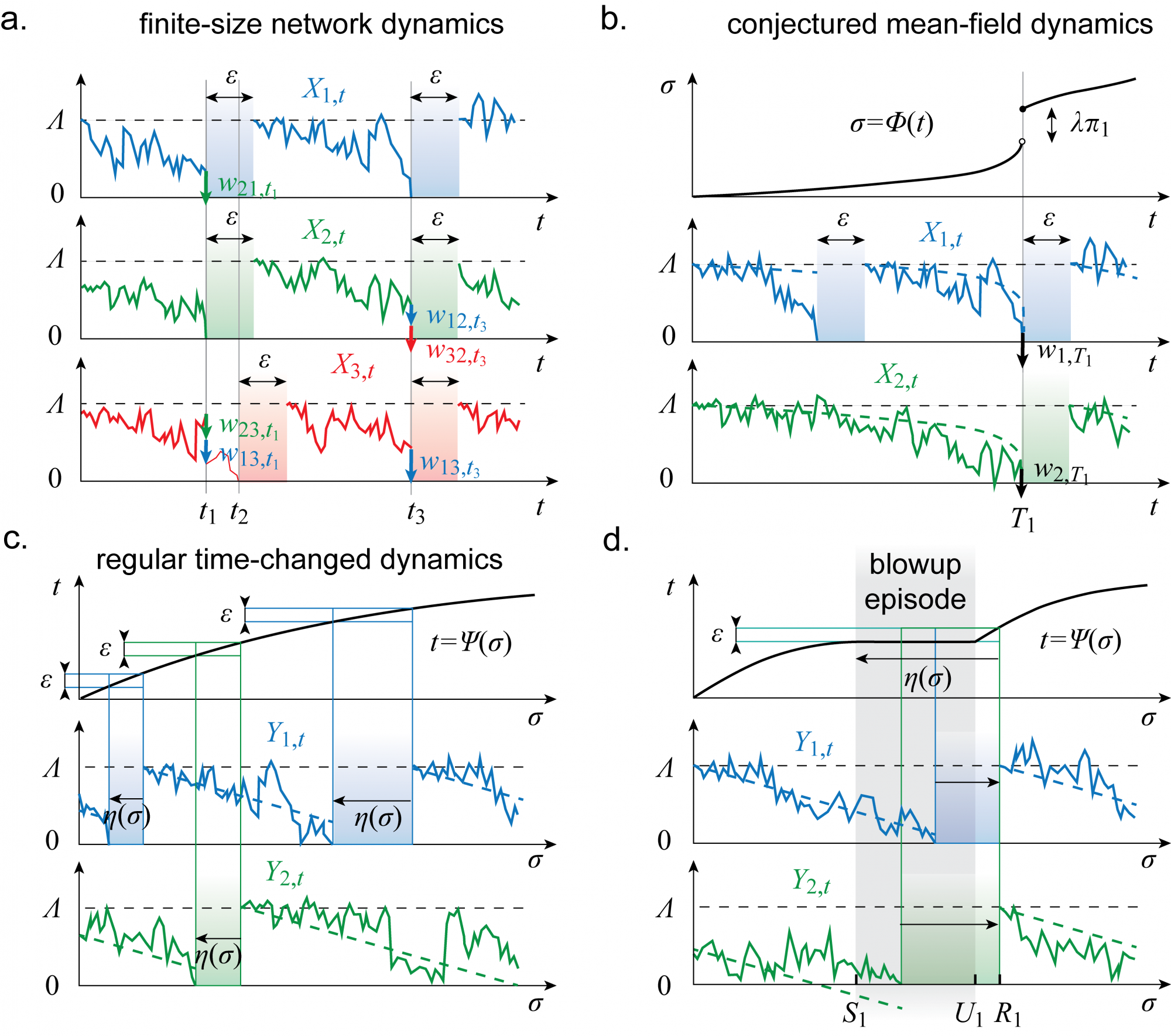
For details, please take a look at this preprint and that preprint, which exhibit Poissonian mean-field dynamics with sustained synchrony. Altogether, these preprints lay down the mathematical foundation for understanding the possible emergence and maintainance of synchrony at the network level in spite of fundamentally noisy neuronal mechanisms. Although Poissonian mean-field networks represent a special class of models, and their analitycal treatment is by no means generic, considering these networks allows one to tackle questions of braod relevance in a well-posed idealized setting. Such questions include, for example, establishing a singular mean-field regime as the limit of some interacting-particle systems, analytically characterizing the breakdown of time-reversibility during the synchronous regime, elucidating the critical regime at the synchrony onset, studying generlized dynamics bearing on heterogeneous populations...